Volume of Revolved Solids
It's all about cylinders.
There are three main formulas for finding the volume of a revolved solid: disk, washer, and shell. If you memorizing these formulas tricky, you are not alone, but there is a mnemonic that we can use to help memorize all the component parts to each formula:
Each formula integrates to the volume of a cylinder.
To find the volume of a cylinder in disk method, we take the are of the circular base of of the cylinder and integrate over the height, dh. Because are integrating over dh, r is considered a constant, and the integral of dh equals just h, and voila, volume of a cylinder formula at the end. And you get the same formula, whether the axis of rotation is vertical or horizontal. Washer method is exactly like disk method, but with an inner cylinder cut out. We integrate two separate areas, one over the larger radius and one over the smaller radius, both over the same dh, and then subtract the smaller volume from the larger volume. And again, this works in either rotational direction, as you can integrate over dy or dx, whichever is in the direction of the height. Shell Method can be a bit trickier to see. Instead of integrating the area of a circle over a straight height line, we now integrate the lateral surface area of the cylinder in the radial direction of the radius.Disk Method
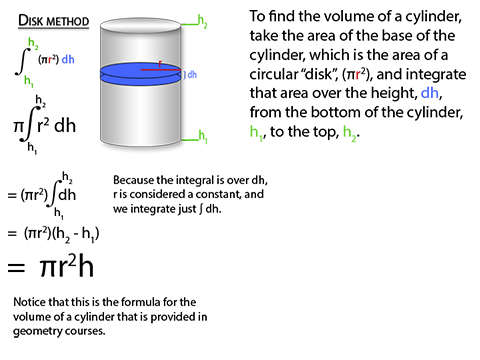
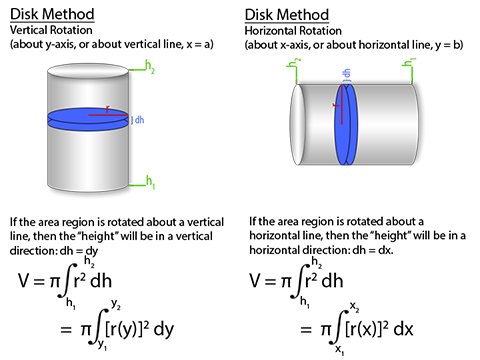
Washer Method
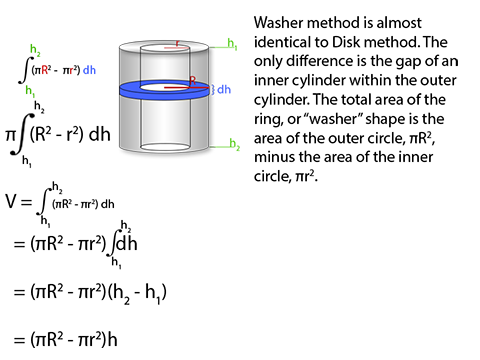
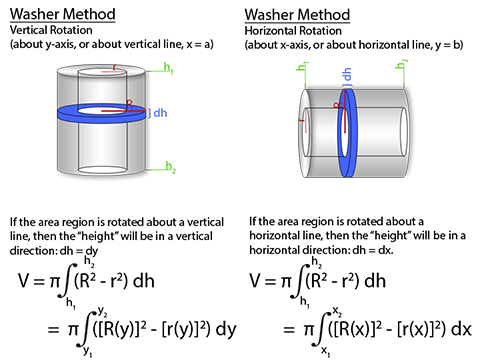
Shell Method

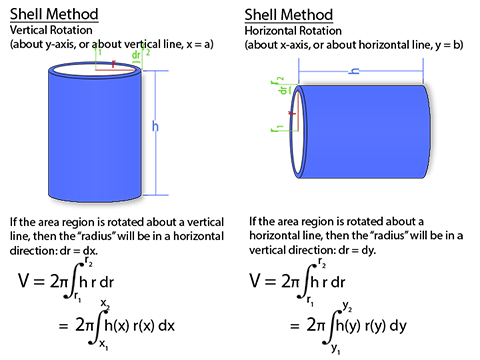
Formulas
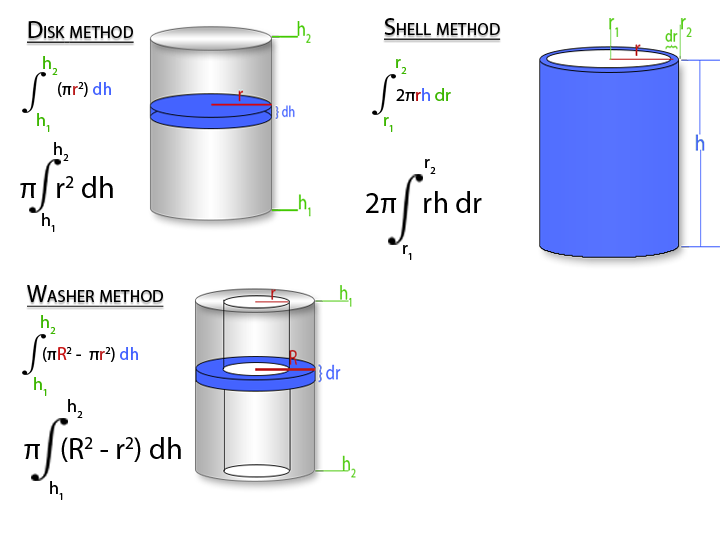
Examples